
新智元报道
编辑:LRST
Adam 优化器是深度学习中常用的优化算法,但其性能背后的理论解释一直不完善。近日,来自清华大学的团队提出了 RAD 优化器,扩展了 Adam 的理论基础,提升了训练稳定性。实验显示 RAD 在多种强化学习任务中表现优于 Adam。
ICLR(国际学习表征会议)是机器学习领域三大顶会之一,以推动深度学习基础理论和技术创新著称。每年,ICLR 时间检验奖都会授予近十年对深度学习领域产生深远影响的里程碑式论文。
今年这一殊荣花落 Adam 优化器(Adaptive Moment Estimation),该算法于 2014 年由 OpenAI 工程师 Diederik Kingma 和 University of Toronto 研究生 Jimmy Ba 提出。
从计算机视觉到自然语言处理,从强化学习到生成模型,Adam 以其卓越的自适应能力,成为当代深度学习模型的「标配」优化器,堪称 AI 领域的「万金油」。

Diederik Kingma 是谷歌的一名研究科学家,曾经是 OpenAI 初创团队的一员,期间领导了基础算法研究团队。2018 年,Kingma 跳槽到谷歌,加入 Google Brain(现为 Google DeepMind),专注于生成式模型研究,包括扩散模型和大型语言模型。他是变分自编码器(VAE)、Adam 优化器、Glow 和变分扩散模型等工作的主要作者。
Jimmy Ba 是深度学习教父 Geoffrey Hinton 的得意门生,于 2018 年获得 University of Toronto 的博士学位。作为 Hinton 学术家族的核心成员,他在 ICLR、NeurIPS 等顶级会议发表多篇开创性论文(其中 Adam 优化器论文引用量已突破 21 万次),堪称 AI 领域最具影响力的青年科学家之一。
Adam 优化器虽在工程实践中表现优异,但长期以来缺乏对其优异性能的理论解释。
近期,清华大学李升波教授课题组发文 《Conformal Symplectic Optimization for Stable Reinforcement Learning》,解析了这一「黑箱」算法的优化动力学机理。
该课题组的研究发现了神经网络优化过程与共形哈密顿系统演化存在「完美」的数学对偶性,揭示了 Adam 优化器暗藏的「相对论动力学」和「保辛离散化」本质,并由此提出了训练更加稳定、性能更加优秀的 RAD 优化器(Relativistic Adaptive Gradient Descent),这一研究工作为神经网络优化动力学的分析及全新算法的设计开辟了新航道。
Adam 优化器的历史与算法特点
神经网络的优化主要依赖梯度下降方法。自 20 世纪 50 年代随机梯度下降(SGD)首次提出以来,优化算法经历了多次重要演进。从动量方法如 SGD-M 和 NAG,到自适应方法如 AdaGrad、RMSprop,优化算法的「演变之战」已持续超过 70 年。
2014 年,Diederik Kingma 与 Jimmy Ba 联合提出了 Adam 优化器(算法1),将神经网络优化算法的性能向前推进了一大步。该算法的核心设计思想是融合 Momentum 和 RMSProp 两大优化方法的优势:
通过指数移动平均计算一阶动量 vk+1 和二阶动量 yk+1,分别估计梯度的一阶矩(即梯度期望)和原始二阶矩(近似于梯度方差)。针对动量零初始化导致的估计偏差,通过引入偏差修正技术,Adam 兼具了快速收敛与稳定训练的双重特性。

从算法原理看,Adam 优化器通过动态维护一阶动量(方向修正)和二阶动量(步长调节),实现了参数更新的双重自适应:既优化了更新方向,又自动调整了有效学习率,显著加速了网络收敛。其偏差修正机制有效消除了训练初期的估计偏差,确保了参数更新的准确性。
此外,Adam 展现出优异的超参数鲁棒性,在大多数场景下无需精细调参即可获得稳定性能。正是这些优势使其成为各类监督学习、强化学习任务的首选优化器。
Adam 优化器为何具备如此出色的训练性能?至今仍缺乏对其优化动力学机理的深入解释,这已成为限制新一代神经网络优化算法设计的关键障碍。
梯度下降过程与动力学演化的对偶机制
受中国科学院院士冯康先生和美国国家三院院士M. I. Jordan 的研究启发(前者开创了哈密顿算法与保辛离散化理论,后者成功将保辛理论引入最优化领域),清华大学的研究团队提出了一种神经网络优化算法的性能理论解释框架:
第一步,将神经网络的参数优化过程对偶为共形哈密顿系统的状态演化过程,建立参数梯度下降与系统能量耗散之间的内在联系。
第二步,利用保辛机制实现共形哈密顿系统的离散化,将离散系统的优势动态特性映射到神经网络的优化过程,从而完成对算法优化动力学的机理解释。
研究发现,神经网络梯度下降过程与共形哈密顿离散系统的演化呈现高度相似性,通过将网络参数θ对偶为系统状态q,目标函数J(θ)对偶为系统势能U(q),可直接建立二者间的对偶关系。
研究者据此开发了一个全新的网络优化算法开发框架,包含两个核心步骤:
1)动能建模:通过设计合适的动能项T(p)以嵌入期望的动态特性;
2)保辛离散:采用保辛离散方法以精确保持系统的动力学性质。
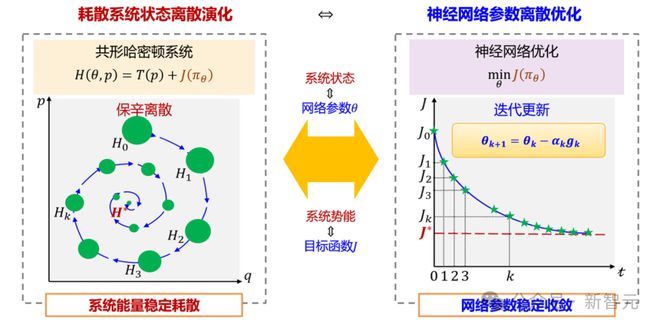
RAD 优化器的设计思路与性能对比
进一步地,研究者将神经网络参数的优化过程建模为多粒子相对论系统状态的演化过程,通过引入狭义相对论的光速最大原理,抑制了网络参数的异常更新速率,同时提供了各网络参数的独立自适应调节能力,从理论上引入了对网络训练稳定性和收敛性等动态特性的保障机制。
这一工作使得研究者提出了既具备稳定动力学特性又适用于非凸随机优化的神经网络优化算法,即 RAD 优化器(算法2)。

研究发现,当速度系数σ=1 且保辛因子ζk取固定小值ε时,RAD 优化器将退化为 Adam 优化器,揭示了 Adam 优化器的动力学机理,说明了 Adam 优化器是新提出的 RAD 优化器的一个特例。
相比于 Adam 优化器,RAD 优化器具有更加优异的长期训练稳定性,这是因为:
1)优化前期:RAD 具有类似 Adam 的快速收敛特性,能够高效定位到最优解的邻域;
2)优化后期:RAD 的保辛结构逐渐增强,具备维持共形哈密顿系统动态特性的能力,确保算法具备更加优异的抗干扰能力。
值得注意的是,Adam 中的有理因子ε是一个「人为引入」的小常数,用于避免分母为零的数值错误。而 RAD 的保辛因子ζ与哈密顿系统的「质量×质能」(即 m2c2)相关,具有明确的物理根源。
这为之前的经验性发现(即适度增加ε可提升 Adam 性能)提供了理论性解释:增大ε使得优化过程更加接近原始的动力学系统。该研究成果不仅深化了 Adam 与动力学系统的本质联系,同时也为分析其他主流自适应优化器(如 AdaGrad、NAdam、AdamW 等)提供了普适性的框架。
为了评估 RAD 优化器的性能,研究者在 5 种主流深度强化学习(DRL)算法(包括 DQN、DDPG、TD3、SAC 和 ADP)和 12 个测试环境(包括 1 个 CartPole 任务、6 个 MuJoCo 任务、4 个 Atari 任务和 1 个自动驾驶任务)中开展了广泛测试,并与 9 种主流神经网络优化器(包括 SGD、SGD-M、DLPF、RGD、NAG、Adam、NAdam、SWATS 和 AdamW)进行了比较,结果表明 RAD 综合性能均排名第一。
特别在图像类标准测试环境 Seaquest 任务中,RAD 性能达到 Adam 优化器的 2.5 倍,得分提升了 155.1%
参考资料:
[1] Lyu Y, Zhang X, Li S E, et al. Conformal Symplectic Optimization for Stable Reinforcement Learning[J]. IEEE Transactions on Neural Networks and Learning Systems, 2024: 1-15.
[2] Kingma D P, Ba J. Adam: A method for stochastic optimization[C]//3rd International Conference on Learning Representations (ICLR). 2015: 1-11.
[3] Li S E. Reinforcement learning for sequential decision and optimal control[M]. Singapore: Springer Verlag, 2023.






