金磊发自凹非寺量子位 | 公众号 QbitAI
天下苦大模型矩阵乘法久矣。
毕竟不论是训练还是推理过程,矩阵乘法作为最主要的计算操作之一,往往都需要消耗大量的算力。
那么就没有一种更“快、好、省”的方法来搞这事儿吗?
有的,香港中文大学最新一篇仅 10 页的论文,便提出了一种新算法:
- 能源可节省:5%-10%
- 时间可节省:5%

论文作者之一的 Dmitry Rybin 表示:
- 这项研究对数据分析、芯片设计、无线通信和 LLM 训练都有着深远的影响!
这么算矩阵乘法,更快!
矩阵乘法是计算机科学和数值线性代数中的核心问题之一。
自从 Strassen 和 Winograd 的开创性工作以来,研究者们一直在探索如何减少矩阵乘法所需的计算量。
尽管这类运算在统计、数据分析、深度学习和无线通信等领域有着广泛应用,例如协方差矩阵的计算和线性回归中的关键步骤,但对于具有特殊结构的矩阵乘法(如计算矩阵与其转置的乘积 XXt)的研究相对较少。
从理论角度看,计算 XXt 与一般矩阵乘法具有相同的渐近复杂度,因此只能通过常数因子优化来提升速度。
因此,这篇论文《XXt Can Be Faster》提出了一种名为 RXTX 的新算法,通过结合机器学习搜索方法和组合优化技术,显著提升了 XXt 的计算效率。

我们先来了解一下 RXTX。
整体来看,这个基于4×4 分块矩阵的递归乘法,通过机器学习搜索与组合优化相结合的方法发现。
算法主要包含以下关键步骤:
- 分块与递归调用
- :将矩阵X划分为 16 个4×4 子块,通过 8 次递归调用处理子问题,并计算 26 个一般矩阵乘积 m1 至 m26。

- 对称乘积计算
- :直接计算 8 个子块的对称乘积 s1 至 m8。
- 结果组合
- :通过线性组合上述乘积结果,得到最终的 XXt 矩阵各分块元素 C11 至 C44。


与此前最先进的算法(基 Strassen 的递归分治)相比,RXTX 的递归关系式为 R (n)=8R (n/4) + 26M (n/4),而原算法为 S (n) = 4S (n/2) + 2M (n/2)。
这一设计使得 RXTX 的渐近乘法常数为 26/41≈0.6341,比原算法的2/3≈0.6667 降低了约5%。
接下来,我们来看下乘法次数与运算总量分析。
通过论文中的定理 1 的推导,RXTX 的乘法次数表达式为:

实验数据表明,当n为 4 的幂次时,RXTX 的乘法次数比原算法低5%,且随着n增大,这一优势持续保持:
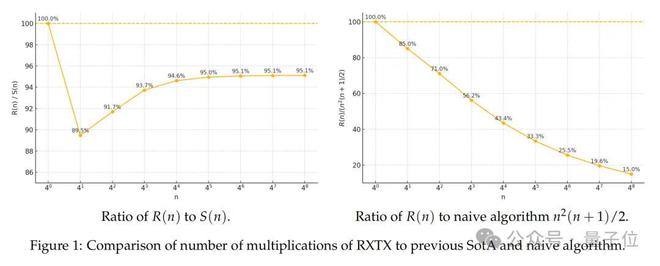
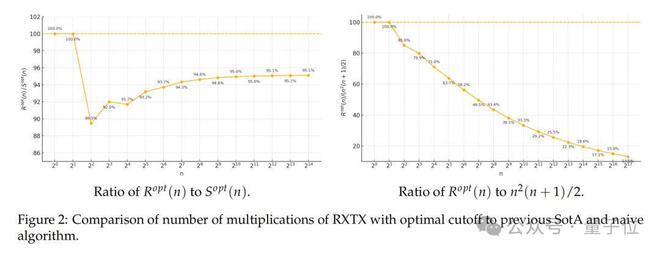
通过优化加法步骤(利用公共子表达式减少加法次数),RXTX 的总运算量表达式为:
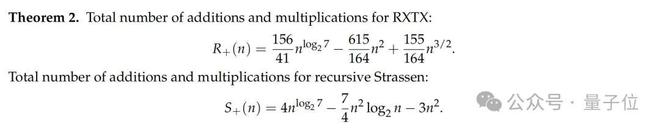
而原算法的总运算量包含对数项,导致其增长更快。
实验显示,当n≥256 时,RXTX 的总运算量优于原算法;当n≥1024 时,显著优于朴素算法:
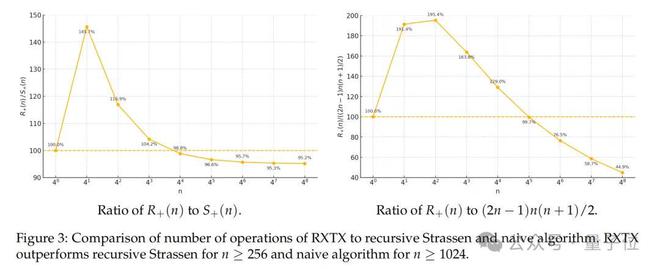
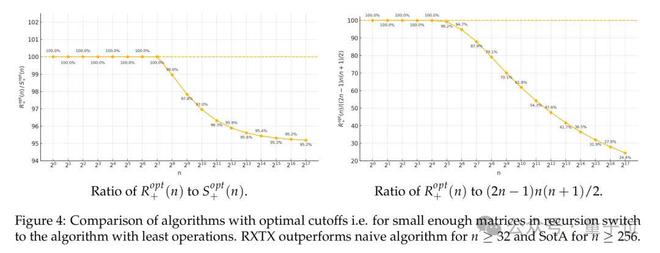
在 6144×6144 矩阵的测试中,RXTX 的平均运行时间为 2.524 秒,比 BLAS 的默认实现快9%,且在 99% 的测试中表现更优:
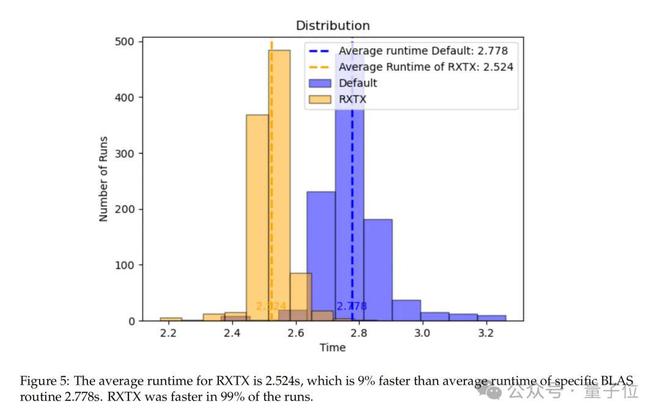
尽管运行时间受硬件和内存管理影响,但理论分析表明,当n≥256 时,RXTX 即可展现速度优势。
值得一提的是,RXTX 的发现得益于机器学习与组合优化的结合,具体流程如下:
- RL 代理生成候选乘积:通过强化学习策略生成大量可能的秩-1 双线性乘积。
- MILP 枚举与筛选:
- MILP-A:枚举候选乘积与目标表达式(XXt 的各分块)之间的线性关系。
- MILP-B:选择最小的乘积子集,确保所有目标表达式可通过线性组合表示。
- 大邻域搜索迭代:通过迭代优化,逐步减少冗余乘积,提升算法效率。
这一方法借鉴了 AlphaTensor 的思路,但通过限制候选空间为二维张量,显著降低了计算复杂度,使得 MILP 求解器(如 Gurobi)能够高效处理。
论文地址:
https://arxiv.org/abs/2505.09814
参考链接:






