PointKAN 团队投稿
量子位 | 公众号 QbitAI
新架构选择用 KAN 做 3D 感知,点云分析有了新 SOTA!

来自哈尔滨工业大学(深圳)和宾夕法尼亚大学的联合团队最近推出了一种基于 Kolmogorov-Arnold Networks(KANs)的 3D 感知解决方案——PointKAN,在处理点云数据的下游任务上展现出巨大的潜力。
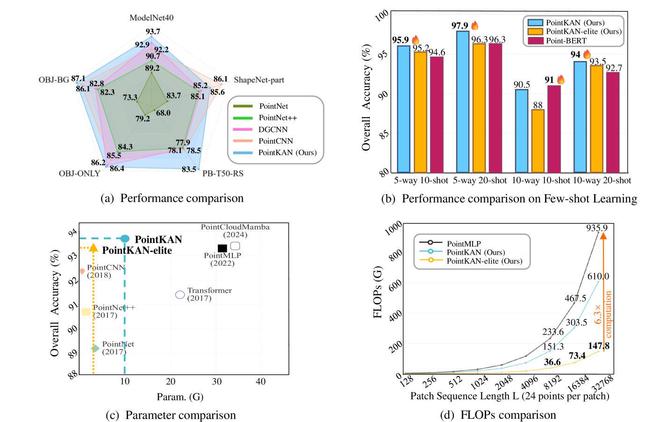
PointKAN 与同类产品的比较
替代传统的 MLP 方案,PointKAN 具有更强的学习复杂几何特征的能力。
此外团队还提出 PointKAN-elite 版本,使用 Efficient-KANs 结构,在保持准确率的同时显著降低参数量。

以下是更多详细内容介绍。
为什么要选择 KANs
当前多层感知机(MLPs)凭借其高效的特征学习机制,已成为点云分析的基础架构组件。
然而在处理点云复杂几何结构时,MLP 的固定激活函数难以有效捕捉局部几何特征,同时存在参数量冗余大、模型效率低下的问题。
而 KANs 是以 Kolmogorov-Arnold 表示定理(KART)作为数学依据的一种新颖的神经网络架构,与多层感知机(MLP)结构的最大区别是 KANs 使用可学习函数替代固定激活函数。
KANs 使用一维B样条函数作为基函数通过相加和复合运算实现高维复杂函数,为函数拟合提供了一个灵活且可解释的框架。
目前,KANs 已初步应用于计算机视觉和医学成像等领域,展现出了有效性和通用性,但在点云分析领域中基于 KANs 的模型拥有巨大潜力尚未开发。
因此,探索在点云分析任务中有效整合 KANs 与现有模型的方法,仍是一个重要且有前景的研究方向。
PointKAN 框架解析
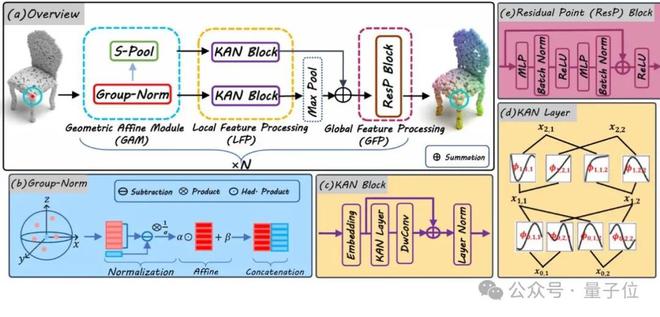
PointKAN 的整体流程如下图所示。
相比于 MLPs,尽管 KANs 具有更强的高维函数逼近能力和更高的参数效率,但将其适配到 3D 点云上并非易事。
一方面,KANs 的样条激活函数通过离散节点逼近单变量函数,很难充分捕捉局部点云的几何特征,限制了其学习细节特征的能力。
另一方面,每一维输入的激活函数需要存储多个参数,对于大规模网络,KANs 的内存需求可能成为瓶颈,并且 KANs 中使用的B样条函数对于现代硬件上的并行计算未进行优化,导致推理速度较慢。
为了解决上述问题,研究团队提出了 PointKAN,其特点是包含几何仿射模块和并行结构的局部特征提取模块,以及 KANs 的高效版本Efficient-KANs来减少内存占用并加快训练和推理速度。
Geometric Affine Module
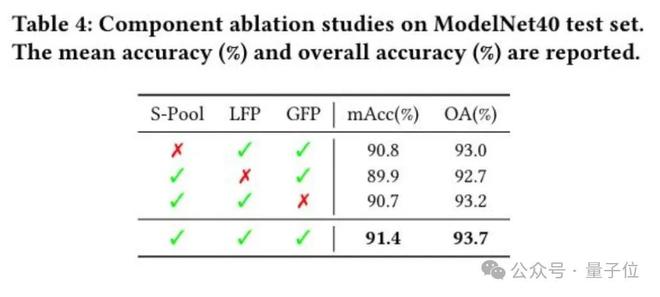
为了在后续的局部特征提取阶段能得到更加丰富的信息,在这个模块中包含两个部分Group-Norm和S-Pool。
Group-Norm 对分组内特征进行归一化、仿射变换和组中心特征传播,整个过程表达如下:
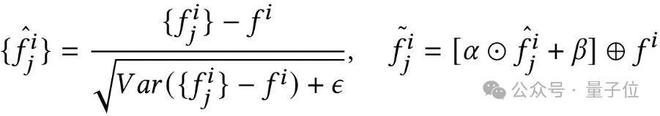
S-Pool 用于对各组特征进行聚合,作为后续模块的输入,对各组点云进行全局信息的补充,考虑到最大池化会导致信息丢失,而S-Pool 则最大限度保留组内各点特征信息,数学形式如下:
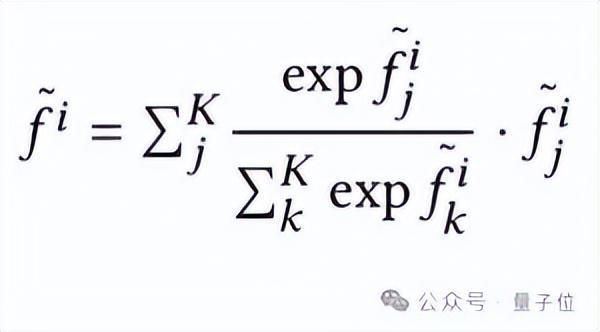
Local Feature Processing
对 Geometric Affine Module 的两部分输出在 Local Feature Progress(LFP)中分别使用KAN Block进行并行处理。
在 KAN Block 中,团队在 KAN Layer 后加上深度卷积(DwConv)操作来协助 KANs 在高维通道信息上学习到丰富的特征表示,整个过程可以被表示为:
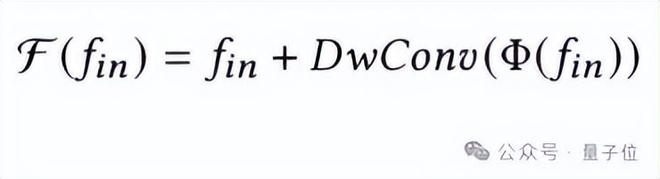
共享的 LFP 旨在从分组点云中学习到局部特征,在经过最大池化后与从各组中心点云学习到的全局信息相加,使得各组点云最终输出的聚合特征更加丰富。
Global Feature Processing
Global Feature Progress(GFP)由 Residual Point(Resp)Block 组成,用于提取深度聚合特征。
由于结构中只包含前馈 MLP,使得可以在 GFP 中添加多个重复 Residual Point(Resp)Block,整个模型仍然能高效运行。
总的来说,代替使用复杂的局部几何提取结构,PointKAN 的一个阶段由Geometric Affine Module、Local Feature Processing和Global Feature Processing三部分组成,通过重复的四个阶段来构造一个层次化处理点云的深度网络。
Efficient-KANs 结构
KANs 中的激活函数是由B样条函数生成的,而B样条函数需要递归计算,这并不适合现代 GPU 的并行计算架构。
在参数量和计算效率上,每个输入-输出对都有不同的参数和基函数,那么随着 KANs 中隐藏层宽度的增加,参数量呈指数增长,这也导致了巨大的计算开销和可扩展性问题。
Efficient-KANs 很好的解决了这些问题,首先使用有理函数代替B样条函数作为 KANs 中的基函数,激活函数如下所示:
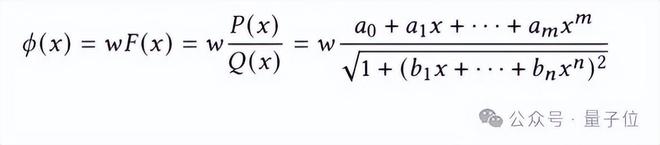
其中的参数通过反向传播进行训练。有理函数计算过程简单,非常适合并行计算,提高了模型的计算效率。
另外 Efficient-KANs 对输入通道进行分组,在组内进行参数共享,来减少参数量和计算量。
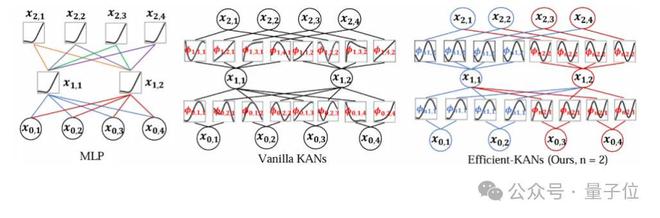
下图展示了 Efficient-KANs、原始 KANs 和标准 MLP 之间的区别。
实验结果
分类任务
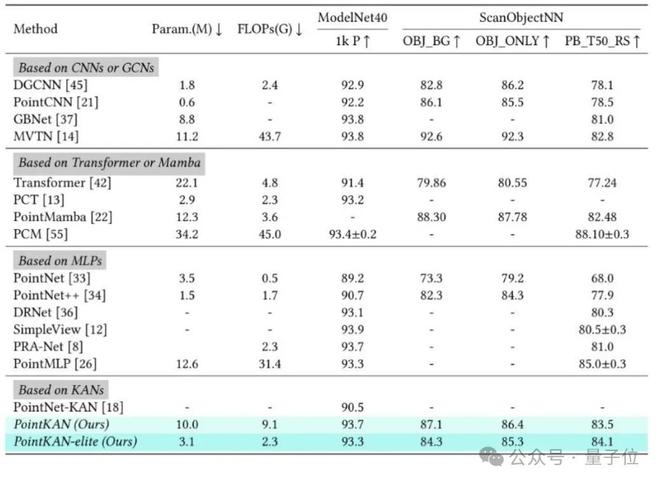
在ModelNet40和ScanObjectNN数据集上进行实验。
部分分割任务
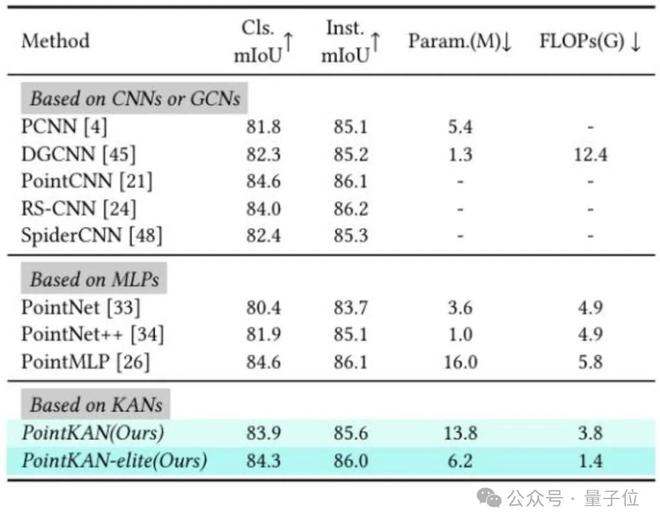
在ShapeNetPart数据集上进行实验。
小样本学习
在ModelNet40数据集上采用“n-way, m-shot”范式进行实验。
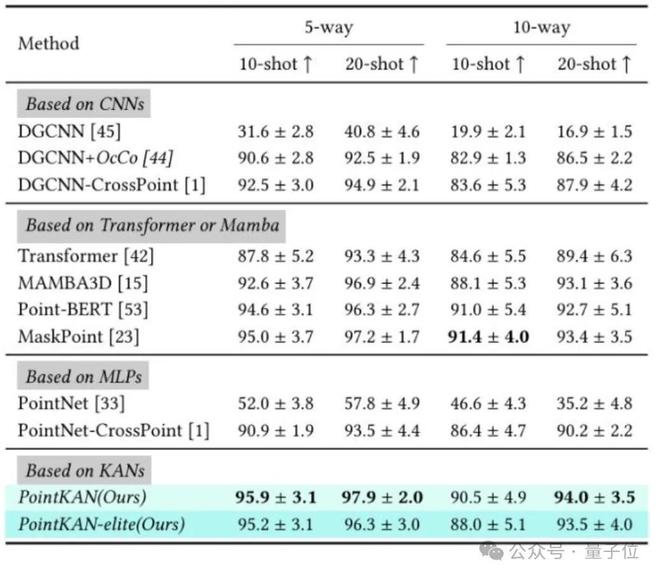
实验结果表明,PointKAN 以及 PointKAN-elite 在各个下游任务上相比于基于 MLPs 的点云分析架构都有出色的表现,特别是在小样本学习任务上,体现了 KANs 具有极强的泛化能力和知识迁移能力,更重要的是参数量和 FLOPs 都有明显的下降。
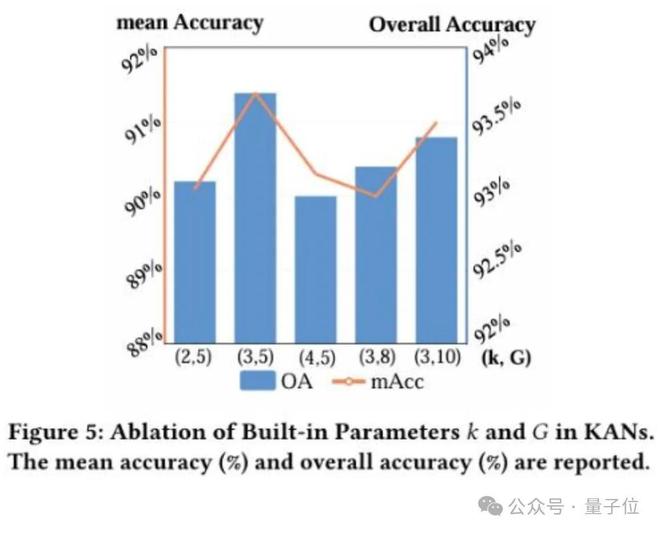
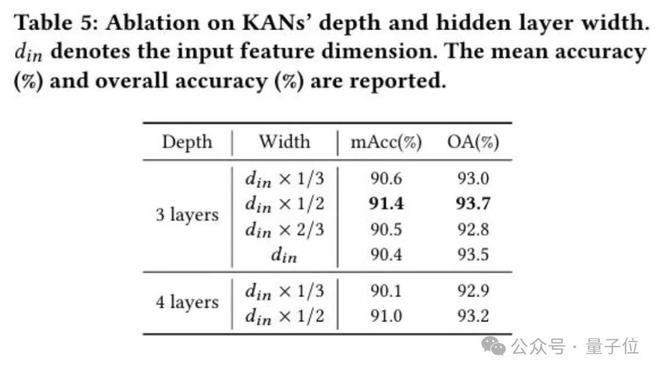
此外消融实验如下图所示:
总结
在本文中,研究人员提出了 PointKAN,一种基于 Kolmogorov-Arnold 网络(KANs)的高效点云分析架构。
相较于基于多层感知机(MLPs)的 PointMLP 架构,PointKAN 在多项任务中均表现出更优性能,充分验证了 KANs 在提取局部细节特征方面的强大能力。
此外,研究团队还提出了更高效的轻量化版本 PointKAN-elite,该版本在保持精度的同时,进一步降低了参数量与计算成本。
团队期待 PointKAN 能够推动 KANs 在点云分析领域的应用,充分发挥其相较于 MLPs 的独特优势。






