
新智元报道
编辑:KingHZ
大模型后训练的痛点:均值优化忽略低概率高信息路径,导致推理能力停滞。RiskPO 双管齐下,MVaR 目标函数推导梯度估计,多问题捆绑转化反馈,实验中 Geo3K 准确率 54.5%,LiveCodeBench Pass@1 提升1%,泛化能力强悍。
当强化学习(RL)成为大模型后训练的核心工具,「带可验证奖励的强化学习(RLVR)」凭借客观的二元反馈(如解题对错),迅速成为提升推理能力的主流范式。
从数学解题到代码生成,RLVR 本应推动模型突破「已知答案采样」的局限,真正掌握深度推理逻辑——
但现实是,以 GRPO 为代表的主流方法正陷入「均值优化陷阱」。
这些基于均值的优化策略,过度聚焦高概率输出序列,却忽略了「低概率但高信息密度」的推理路径:
模型训练早期就会出现熵坍缩,过早丧失探索能力;
面对全错的难题时,优势函数直接归零,模型在薄弱环节完全无法学习。
最终结果是,大模型看似在 Pass@1 等短视指标上有提升,实则推理边界从未拓宽,更无法应对 AIME 竞赛题、复杂代码生成这类高难度任务。
如何让模型主动「啃硬骨头」,成为大模型后训练的关键瓶颈。
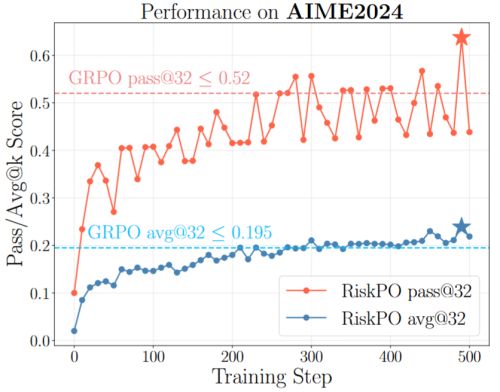
AIME2024 上的学习表现
用「风险度量」破局,
MVaR+ 捆绑策略双管齐下
为解决传统均值优化的缺陷,北大团队提出的 RiskPO,核心突破在于将风险规避(risk-averse)理念融入优化目标,用「关注奖励分布左尾(难任务)」替代「追求整体均值」,从根本上引导模型突破推理短板。

论文链接:https://arxiv.org/abs/2510.00911v1
代码链接:https://github.com/RTkenny/RiskPO
单位:由北京大学彭一杰教授课题组完成
作者:第一作者为任韬,共一作者为江金阳,其他作者包括杨晖等。
这一思路的核心载体是「混合风险价值(MVaR)」目标函数。
团队首先基于区间风险价值(RVaR)构建基础——对于奖励分布,其α/β分位数区间内的 RVaR 定义为该区间内奖励的条件期望,公式为:
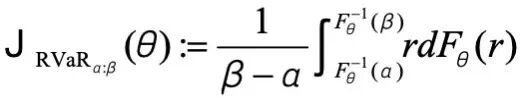
在此基础上,MVaR 通过引入权重参数,进一步放大左尾(低奖励、难任务)的梯度信号,形成最终目标:
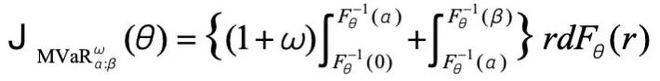
其中即为对左尾区间的额外关注权重,确保模型优先优化难任务。
为让该目标可落地,团队还严谨推导了 MVaR 的梯度估计式子——基于策略梯度的似然比求导方法,最终得到(式中为捆绑后的总奖励):
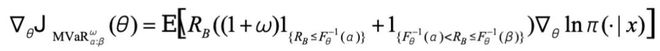
为配合 MVaR 目标,团队提出「多问题捆绑」策略,将多个问题打包成 bundle 计算奖励,把稀疏的二进制反馈转化为更丰富的分布信号,彻底解决「难题零梯度」问题——比如将 5 个数学题打包后,模型能从整体得分中捕捉到「部分正确」的学习信号,而非单个题目非对即错的极端反馈。
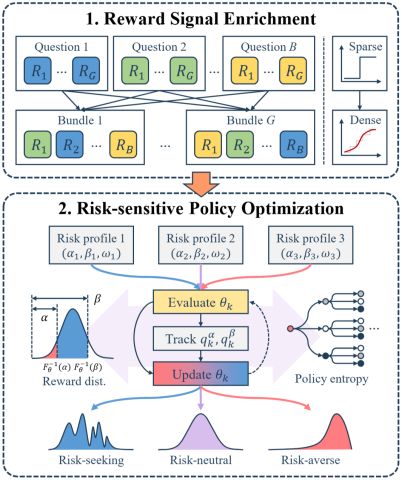
算法架构图
三大任务全面碾压,
难问题上优势更显著
好的技术方案,终要靠硬指标说话。
北大团队在数学推理、代码生成、多模态推理三大领域的 10 余个数据集上,用数据证明了 RiskPO 的突破性——
尤其在最能体现推理能力的「硬任务」上,优势远超 GRPO 及其变体。
在数学推理领域,RiskPO 在 AIME24(美国数学邀请赛)任务上表现惊艳:
Pass@32 得分比 GRPO 高出近 7 个百分点,比最强基线 DAPO 提升 6.7 个百分点;
即便是相对简单的 MATH500 数据集,其 Pass@1 也达到 81.8%,超出 GRPO2.6 个百分点。
更关键的是,随着评估指标从 Pass@1 转向 Pass@8、Pass@16,RiskPO 的优势持续扩大——
这意味着模型不仅能给出更优的单条答案,还能探索更多有效推理路径,真正突破了「采样效率优化」的局限。
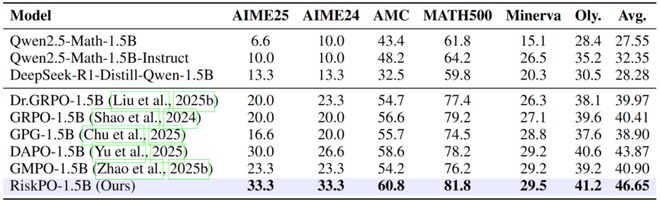
数学推理任务
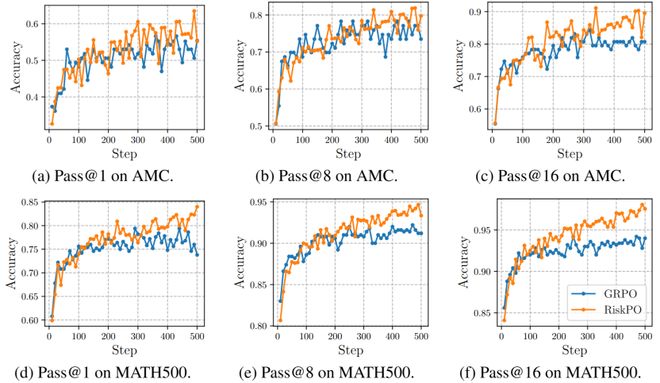
Pass@k学习曲线
在跨领域任务中,RiskPO 同样稳定领先:代码生成任务 LiveCodeBench 上,Pass@1 比 GRPO 提升 1 个百分点;多模态几何推理任务 Geo3K 上,准确率达到 54.5%,优于 DAPO 的 54.3%。这种「全场景增益」,证明了风险度量优化的泛化能力。
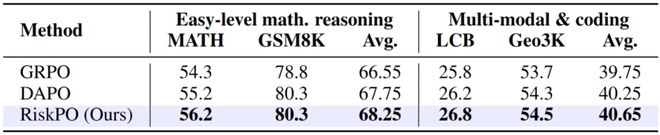
其他任务
熵坍缩缓解有依据
参数设计有章法
RiskPO 的性能突破,并非依赖工程调参,而是有扎实的理论支撑和严谨的消融实验验证。
高熵更新定理:
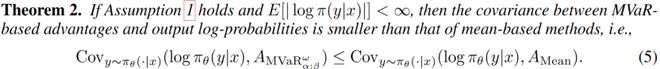
从理论层面,团队证明了「风险规避更新」能有效缓解熵坍缩:通过分析策略熵的变化机制,发现 RiskPO 的 MVaR 目标函数能降低「优势-对数概率」的相关性——相比 GRPO,模型不会过度强化已掌握的易任务,从而保持更高的熵值和探索能力。实验中也能清晰看到:训练 500 步后,GRPO 的熵值已趋近于0,而 RiskPO 仍能维持 0.2 以上的熵水平,确保对难任务的持续探索。
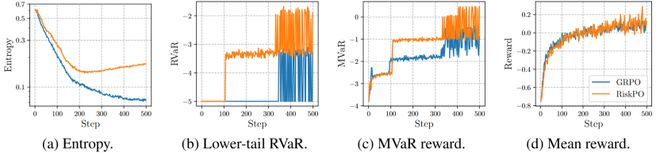
训练集 DAPOMATH-17k 上的各项指标
值得注意的是,在训练过程中,若仅观察以均值为核心的指标曲线(如平均奖励),GRPO 与 RiskPO 的表现几乎难分伯仲,甚至 RiskPO 因更高的探索性还伴随轻微波动;但切换到风险敏感指标(如下尾 RVaR、MVaR 奖励)时,两者差距立刻凸显——RiskPO 的曲线始终保持显著领先,且随训练推进持续攀升。
这种「均值相近、风险指标悬殊」的现象,再结合最终测试集上 RiskPO 在 Pass@k(尤其是高k值)、难任务(如 AIME 竞赛题)上的优势,进一步印证了:均值目标只能让模型在「已知能力范围内优化采样效率」,而风险度量目标才是推动模型突破推理边界、真正提升核心能力的理想方向。
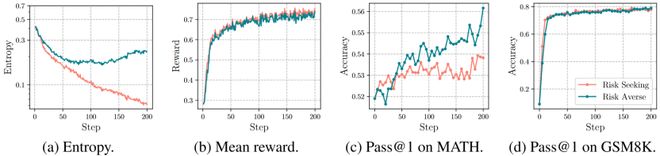
不同风险偏好对比实验
为进一步验证风险规避目标的必要性,团队还设计了「风险寻求(risk-seeking)」对比实验:采用与 MVaR 结构对称的风险寻求目标,即
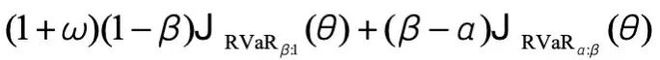
,
重点关注奖励分布的右尾(易任务)。结果显示,风险寻求模型的熵值在训练早期就剧烈坍缩——训练 150 步后熵值已降至 0.1 以下,远低于 RiskPO 的 0.2;性能上,风险寻求模型在训练 50 步后便进入平台期,MATH 数据集 Pass@1 仅从 52% 提升至 54%,而 RiskPO 则持续优化至 56%,实现 1.5 倍的提升幅度。
这一对比清晰证明,聚焦易任务的风险寻求策略会加速模型「固步自封」,只有风险规避才能驱动模型突破推理边界。
参考资料:






